Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
With the year of the snake well underway I welcome you to the Transum Newsletter for the month of February 2025, a month with exactly 8! (eight factorial) minutes. It begins, as usual, with the puzzle of the month.
How many different asymmetrical triangles can be drawn by joining three of the vertices of a regular hexagon?

If you get an answer I'd love to hear how you solved the puzzle (or your students solved it). Drop me an email at: gro.musnarT@rettelsweN
While you think about that, here are some of the key resources added to the Transum website during the last month.
Subscriber Sharon suggested three more panels for the exceedingly popular Refreshing Revision. As you may know, as the teacher, you can choose any number of topics for a projectable Starter customised for your class. The system randomly chooses quick questions on each of those topics for your students to think about. I personally use it in most of my lessons.
Tree Diagram Creator: I often find myself needing to quickly sketch a probability tree diagram to represent a situation and it is often difficult to get the spacing right to account for each of the possibilities. This handy tool, for Transum subscribers only, does the spacing for you so that your visual aid looks more organised.
By the way, how many apples and how many bananas were in the basket according to the tree diagram in the image above (assuming one fruit was taken and not replaced before a second fruit was picked at random)?
Square Numbers is a new interactive resource focused on developing fluency with square numbers. The six-level progression guides students from basic one-digit squares through to more challenging two-digit calculations, with each level building systematically on previous learning. Level 3 features a timed challenge that helps students develop both accuracy and automaticity, presenting randomly generated numbers between 1 and 12 to be squared.
Complements to 100: This straightforward yet engaging activity offers opportunities for learners to practise identifying pairs of numbers that sum to 100, helping them develop greater confidence and fluency in their basic number work. There is an element of randomness in the generation of many of the questions, enabling two students using separate devices to work on this exercise together without being tempted to simply copy each other’s answers. Their discussion will focus on methods rather than outcomes. This same randomness, found in many Transum exercises, also makes it worthwhile for learners to revisit the activity on different days to consolidate their understanding and hone their skills.
Circle Parts: Is moving better than still? Would this dynamic visual aid help learners appreciate the number of different shapes a sector can take? Can a segment be a semicircle? What do major and minor mean? I hope this resource, designed to be projected for whole class exposition, is useful to you.
Apart from half-term there is not a lot for your February diary. All I have is that the 5th February has a palindromic date and that there is a Starter designed for Valentine's Day on the 14th.
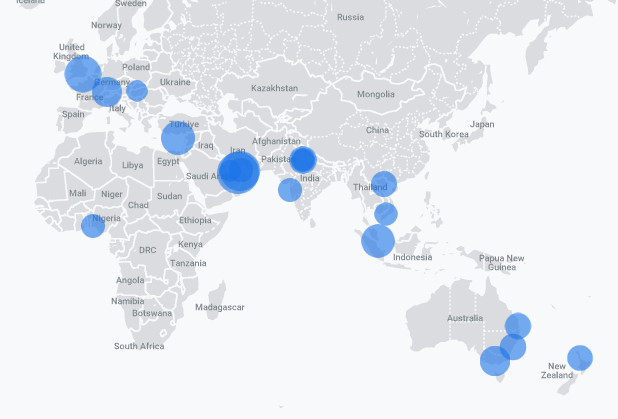
I have noticed that early in the afternoon here in Thailand, I can look at my Analytics dashboard and see the blue circles indicating groups of people accessing Transum around the globe. Apart from a distinctive outlier, the positions of the circles seem to indicate a strong negative correlation between longitude and latitude. Is this meaningful, or have I simply been a Maths teacher for too long?
I often receive interesting mathematical ideas from my friend Allan, who teaches at an international school in Germany. He learnt a couple of German shape names:
He then asked why, in English, we use triangle more often than trilateral and quadrilateral more often than quadrangle. I had never thought about that before, so I consulted the technology at our fingertips and found that it’s mostly a matter of convention and historical preference rather than strict logic.
1. “Triangle” vs. “Trilateral”
Triangle (from tri- meaning ‘three’ and angulus meaning ‘corner’ in Latin) is the standard geometric term for a three-sided polygon.
Trilateral more often appears in contexts referring to political or diplomatic arrangements (for example, a trilateral agreement), rather than geometry.
2. “Quadrilateral” vs. “Quadrangle”
Quadrilateral (from quadri- meaning ‘four’ and latus meaning ‘side’ in Latin) is used as the principal geometric term for a four-sided polygon.
Quadrangle (also from ‘four’ + ‘angle’) has taken on a more architectural or spatial sense—think of courtyards or college quads enclosed by four walls or buildings.
Finally, the answer to last month's puzzle, which was:
It’s the end of the morning break at Addwell School, and ten classrooms, packed with enthusiastic students, are waiting for their next lesson to begin.
Ten teachers leave the staffroom one by one after consuming their morning coffee. The first to leave is Professor Hamnee Shah, who can’t remember which class he is timetabled to teach, so he chooses a class at random and begins teaching them.
The second teacher does the following: goes to their timetabled classroom. If there is no teacher inside, they teach their scheduled class. Otherwise, they choose a random class with no teacher and begin teaching. Every one of the remaining eight teachers does the same. What is the probability that the last teacher out of the staffroom (Ms Lattelike) teaches their timetabled class?
The probability that Ms Lattelike teaches in her timetabled classroom is 50%.
My first instinct was to simplify the problem. If instead of ten teachers there were only two, it would be easy to draw a tree diagram of the situation. the number in the yellow box is the class number - teacher 1 is timetabled to teach class 1 etc:
Two Teachers
The probability that the second teacher gets class 2 is 50%.
I then increased the number of teachers involved:
Three Teachers
The probability that the third teacher gets class 3 is 50%.
Four Teachers
The probability that the fourth teacher gets class 4 is 50%.
I think I see a pattern here!
Here's another way to think about this puzzle:
Suppose that whenever a teacher finds their classroom taken, they politely evict the wrong teacher and take their own class as scheduled. In this scenario, the first teacher (Hamnee) keeps getting evicted and must choose a new random class each time. Eventually, by the time all the other teachers have left the staff room, Hamnee is forced—by process of elimination—into his scheduled classroom.
This scenario is the same as the original process except for the identities of the people in the classrooms, so the probability of the last teacher finding their classroom already occupied is unchanged.
When the last teacher leaves the staff room, Hamnee is either in his own classroom or in the last teacher's classroom, each equally likely, which again leads to a probability of 50%.
This puzzle was an adapted version of the Airplane Seating puzzle.
While the main puzzle of the month proved to be the hardest puzzle yet (due to the lack of solutions received) there was an easier supplementary puzzle which was:
In a room of 100 people, 99% are left-handed. How many left-handed people have to leave the room to bring that percentage down to 98%?
The answer to that was 50.
So the first five communications I received about either of the puzzles came from Rick, Robynn, Allan, Kevin and Shreyak. Thanks to everyone who took part.
That's all for now,
John
P.S. Are monsters good at mathematics?
Not unless you Count Dracula.
Rick,
Thursday, January 2, 2025
"I believe the answer is 50 percent.
I have no idea how to approach the solution mathematically. Probability is one of my mathematical weaknesses. Instead, I created an Excel workbook with four worksheets. I started with a school with only two teachers and two classes, then three, four, and finally five teachers and classes. In each worksheet, I listed all the combinations and then used a formula in cell D3 to calculate the percentage of times the last teacher was successful dividing by the total number of combinations. In each case, the number was 50 percent. Since this was quite tedious to create as the number of classes and teachers grew, I considered writing a Python script for the actual problem with 10 classes and teachers, but I think the pattern will hold, so I will most likely not do this. Another interesting tidbit was that the last teacher either got to teach their class or the first teacher’s class.
I have attached my spreadsheet. Row five is a header row representing a particular teacher. In retrospect, these should have been labelled T1, T2, and so on. Then, rows following contain which class a teacher chose. So, for example in row 6, teacher 1 chooses class 1, and therefore all other teachers choose their correct class."
Rick,
Monday, January 27, 2025
"I have done some more thinking regarding the January puzzle.
First, let’s start with two extremes. If Professor Shah chooses his regular classroom, then all other teachers go to their respective classrooms and Ms Lattelike teaches in her assigned classroom. However, if Professor Shah chooses Ms Lattelike’s classroom, then all other teachers teach in their correct classroom and Ms Lattelike is left with Professor shah’s classroom, hence she does not teach in her classroom. So, for these two extremes, the probability is 50 %.
Now, let’s assume that Professor Shah chooses another classroom. If he chooses the classroom of the teacher who leaves second, then the second teacher is in the same situation as Professor Shah. If he chooses another classroom, then all teachers up to that classroom will teach in their own room, so it is not until the teacher who has a conflict will need to choose at random, same as Professor Shah. Hence, teachers who encounter a conflict will present Ms Lattelike with a 50%probability or pass that opportunity to another teacher. A perfect example of a recursive algorithm. "