Curriculum
The English national curriculum for mathematics aims to ensure that all pupils reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language.
Proof
A mathematical proof is a sequence of statements that follow on logically from each other that shows that something is always true. Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in all possible cases.

Lesson Starter
Introduce the notion of proof with this challenge involving odd numbers - then when the students are convinced it is impossible show them the trick!

Congruent Triangles
Test your understanding of the criteria for congruence of triangles with this self-marking quiz.

Four Colour Theorem
Show that no more than four colours are required to colour the regions of the map or pattern so that no two adjacent regions have the same colour.

Identity, Equation or Formula?
Arrange the given statements in groups to show whether they are identities, equations or formulae.
Line Drawings
Six line drawings that may or may not be able to be traced without lifting the pencil or going over any line twice.

Mix and Math
Determine the nature of adding, subtracting and multiplying numbers with specific properties.
Not Too Close
The students numbered 1 to 8 should sit on the chairs so that no two consecutively numbered students sit next to each other.
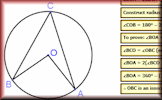
Proof of Circle Theorems
Arrange the stages of the proofs for the standard circle theorems in the correct order.

Satisfaction
This is quite a challenging number grouping puzzle requiring a knowledge of prime, square and triangular numbers.

True or False?
Arrange the given statements in groups to show whether they are always true, sometimes true or false.

Fermat's Last Theorem
Find out about that famous theorem that was mentioned in the margin of a book but took many years to prove.
🔰
Exam-style Question
State whether each of the following statements is true or false. Give reasons for your answers.
🔰
Exam-style Question
One is added to the product of two consecutive positive even numbers. Show that the result is a square number.
🔰
Exam-style Question
Given that \(n\) can be any integer such that \(n \gt 1\), prove that \(n^2 + 3n\) is even.
🔰
Exam-style Question
Use algebra to prove that \(0.3\dot1\dot8 \times 0.\dot8\) is equal to \( \frac{28}{99} \).
🔰
Exam-style Question
The diagram shows a quadrilateral ABCD in which angle DAB equals angle CDA and AB = CD.
🔰
Exam-style Question
(a) Prove that the recurring decimal \(0.\dot2 \dot1\) has the value \(\frac{7}{33}\)
🔰
Exam-style Question
(a) Prove that the product of two consecutive whole numbers is always even.
🔰
Exam-style Question
The number \(T\) can be expressed as \(T = 4k + 3\) where \(k\) is a positive integer.
🔰
Exam-style Question
Using mathematical induction and the definition \( ^nC_r = \frac{n!}{r!(n-r)!} \), prove that
🔰
Exam-style Question
Prove that the integers \(a\) and \(b\) cannot both be odd if \(a^2+b^2\) is exactly divisible by 4.
💢
Advanced Starter
Divisible by 11
Can you prove that a three digit number whose first and third digits add up to the value of the second digit must be divisible by eleven?
💢
Advanced Starter
Key Eleven
Prove that a four digit number constructed in a certain way will be a multiple of eleven.
💢
Advanced Starter
Log Perfection
Determine whether the given statements containing logarithms are true or false
Syllabus
📘
See the requirements for the International Baccalaureate Anaylsis and Approaches Standard Level Mathematics course.
Syllabus
📘
See the requirements for the International Baccalaureate Anaylsis and Approaches Higher Level Mathematics course.
Syllabus
📙
See the content for Mathematics AS and A level as published by the UK's Department for Education.
Tip
💡
If \(n\) is a whole number then \(2n\) is an even number.
If \(n\) is a whole number then \(2n + 1\) is an odd number.
Tip
💡
positive × positive = positive
positive × negative = negative
negative × positive = negative
negative × negative = positive
Tip
💡
even × even = even
even × odd = even
odd × even = even
odd × odd = odd
Tip
💡
To prove something is not true you only need to find one counterexample.
Tip
💡
To prove an identity is true show that the left-hand side (LHS) is equal to the right-hand-side (RHS).
Tip
💡
Finally here are three letters to conclude your proof:
QED is an initialism of the Latin phrase quod erat demonstrandum, meaning "which was to be demonstrated".